Introduction
In the labyrinthine realm of economics, the price weighted index (PWI) stands as a beacon, guiding investors, analysts, and economists alike through the fluctuations of the market. This metric, like a celestial navigator, charts the course of inflation, economic growth, and consumer behavior. In this comprehensive guide, we embark on a journey to unravel the intricacies of the PWI, empowering you with the knowledge to calculate it with precision and interpret its multifaceted implications.
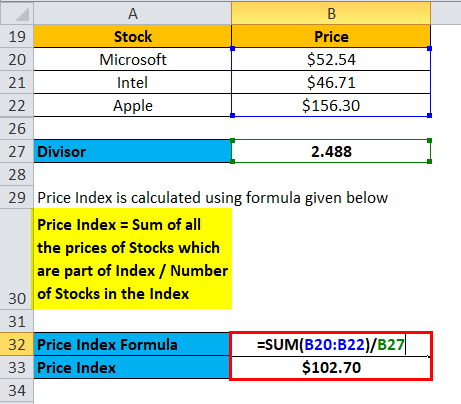
Image: www.regency.com.co
Understanding the Price Weighted Index
At its core, the PWI gauges the overall change in a basket of goods and services over time. Unlike its cousin, the Laspeyres index, the PWI employs a dynamic approach, adjusting the weights of individual items based on their current prices. This fluidity grants the PWI an edge in capturing the shifting landscape of consumer spending patterns.
Calculating the Price Weighted Index
The formula for calculating the PWI is a testament to its simplicity and elegance:
PWI = (∑(Pt x Qo)) / (∑(Po x Qo))
Where:
- Pt represents the current price of an item
- Qo signifies the base quantity of that item
- Po denotes the base year price
In essence, the PWI multiplies the current price of each item by its base year quantity, sums these values, and divides the total by the aggregate of base year prices multiplied by base year quantities.
Example: Putting the Formula into Practice
Consider a basket of goods comprising apples, oranges, and bananas. The base year prices and quantities are as follows:
| Item | Base Year Price (Po) | Base Year Quantity (Qo) |
|---|---|---|
| Apples | $1 | 100 lbs |
| Oranges | $2 | 50 lbs |
| Bananas | $3 | 25 lbs |
In the current year, the prices have shifted:
| Item | Current Price (Pt) | Base Year Quantity (Qo) |
|---|---|---|
| Apples | $1.50 | 100 lbs |
| Oranges | $2.50 | 50 lbs |
| Bananas | $3.50 | 25 lbs |
Plugging these values into the formula, we get:
PWI = (∑(Pt x Qo)) / (∑(Po x Qo))
= (($1.50 x 100) + ($2.50 x 50) + ($3.50 x 25)) / (($1 x 100) + ($2 x 50) + ($3 x 25))
= $325 / $250
= 1.3
This result (1.3) indicates that the overall price level of this basket of goods has increased by 30% since the base year.
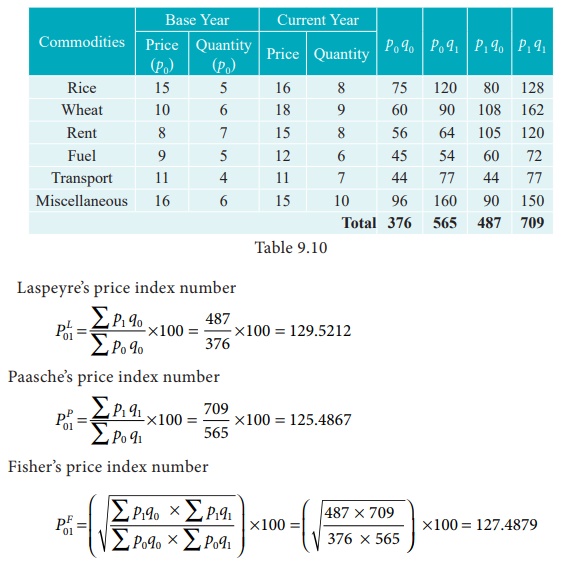
Image: rhayzlzenia.blogspot.com
Applications of the Price Weighted Index
The PWI plays a pivotal role in manifold economic analyses and policy decisions:
- Inflation Measurement: As a key component of the Consumer Price Index (CPI), the PWI provides a reliable measure of inflation, informing monetary policies and economic forecasting.
- Economic Growth Assessment: By tracking price changes over time, the PWI assists economists in gauging economic growth, identifying potential imbalances, and formulating fiscal policies.
- Portfolio Management: Investors leverage the PWI to assess the inflation risk associated with their portfolios, guiding asset allocation decisions and safeguarding their investments.
- Consumer Behavior Analysis: Marketers and policymakers use the PWI to understand consumer spending habits, pinpointing areas of demand growth and identifying opportunities for product innovation.
Limitations of the Price Weighted Index
While the PWI offers valuable insights, it is not without limitations:
- Susceptibility to Substitution Bias: The PWI assumes consumers do not switch to cheaper alternatives, which may not always be the case in practice.
- Inapplicability to New Products: New products, absent from the base year basket, are not accounted for in the PWI, leading to potential inaccuracies.
- Sensitivity to Sample Selection: The choice of goods and services in the basket can significantly impact the PWI, emphasizing the importance of representative sampling.
Recent Developments and Future Outlook
The PWI has continually evolved in response to changing economic landscapes. Recent developments include:
- Hedonic Regressions: Economists now use hedonic regressions to adjust for quality changes in products, refining PWI calculations and enhancing accuracy.
- Superlative Indices: Researchers have introduced more sophisticated indices, such as the Fisher Index and Törnqvist Index, that provide alternative approaches to capturing price level changes.
As technology advances and economic dynamics shift, future developments in PWI calculation methods hold the potential to further enhance the precision and adaptability of this indispensable metric.
How To Calculate Price Weighted Index
Conclusion
The PWI, an essential tool in the economic arsenal, empowers us to track inflation, monitor economic growth, and analyze consumer behavior patterns. Its simplicity and flexibility, coupled with its interpretability, make it accessible to a wide range of users. By delving into the intricacies of the PWI, we gain a deeper comprehension of the dynamic forces that shape the economy and empower ourselves to make informed decisions in the face of market fluctuations.