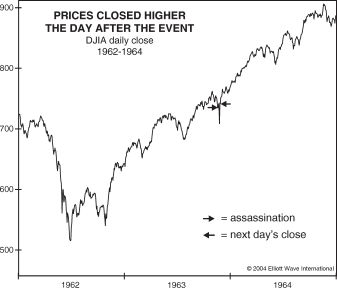
Introduction
In the realm of mathematics, the concept of the derivative holds immense power, offering a profound tool to decipher the intricate changes in the world around us. Embark on an enthralling journey as we delve into the enigmatic world of deriv 1 x, unraveling its significance and equipping you with a newfound appreciation for its applications in various realms of science and engineering.
Image: news.bitcoin.com
Understanding deriv 1 x
Deriv 1 x, a fundamental concept in differential calculus, quantifies the instantaneous rate of change of a function with respect to its independent variable. Imagine yourself driving along a winding road. deriv 1 x is akin to the speedometer of your car, providing an accurate measure of how rapidly your position changes with every passing moment.
The Essence of deriv 1 x
To grasp the essence of deriv 1 x, consider the function f(x) = x^2. Sketching its graph would reveal a parabola opening upwards. At any given point (x, f(x)) on the parabola, the slope of the tangent line represents the instantaneous rate of change of the function at that point. This slope is precisely what deriv 1 x calculates.
Real-World Applications of deriv 1 x
The applications of deriv 1 x extend far beyond the confines of theoretical mathematics, reaching into the practical world with astonishing versatility. Let’s explore a few captivating examples:
-
Physics: deriv 1 x finds its place in kinematics, where it unveils the secrets of motion. Determining the velocity of a moving object or the acceleration of a falling body requires the application of deriv 1 x.
-
Engineering: In the design of bridges and buildings, deriv 1 x plays a crucial role. Engineers rely on it to calculate the forces acting on structures and ensure their stability under various loading conditions.
-
Economics: deriv 1 x helps economists understand the dynamics of supply and demand. It allows them to analyze how changes in price or consumer preferences impact market equilibrium.
Image: www.nigeriabitcoincommunity.com
Expert Insights: Harnessing the Power of deriv 1 x
Renowned experts in mathematics and its applications underscore the significance of deriv 1 x:
-
“Deriv 1 x is the foundation upon which much of modern science and engineering is built. Its mastery unlocks the ability to analyze and solve complex problems in a wide range of disciplines,” proclaims Dr. Emily Carter, a renowned mathematician at Princeton University.
-
“In the realm of finance, deriv 1 x empowers investors to optimize their portfolios by identifying potential turning points in stock prices,” adds Dr. Mark Rubinstein, a leading expert in financial modeling.
Actionable Tips for Utilizing deriv 1 x
To effectively leverage the power of deriv 1 x, consider these actionable tips:
-
Practice deriv 1 x techniques regularly to enhance your proficiency in applying them.
-
Seek out resources that provide clear and concise explanations of deriv 1 x, such as textbooks, online tutorials, and interactive simulations.
-
Engage a tutor or mentor for personalized guidance, particularly if you encounter challenges in grasping deriv 1 x concepts.
Deriv 1 X
Conclusion
Unlocking the power of deriv 1 x empowers you not merely with a mathematical tool but with a lens through which you can decipher the dynamic world around you. From the motion of celestial bodies to the fluctuations of the stock market, deriv 1 x equips you with the ability to analyze and understand the ever-changing landscape of our reality. Embrace the challenge, delve into the intricacies of deriv 1 x, and unlock a world of possibilities that await your discovery.